Как ресемплить томографические данные

1171 слов · 6 мин.

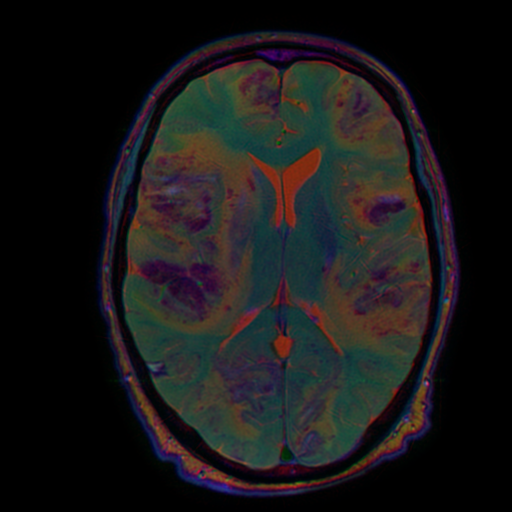
Когда мы работаем с задачей классификации или сегментации каких-то МРТ-данных, то сталкиваемся с тем, что серии с разной взвешенностью нарезаны в разных плоскостях и с разной толщиной среза. Это можно исправить.

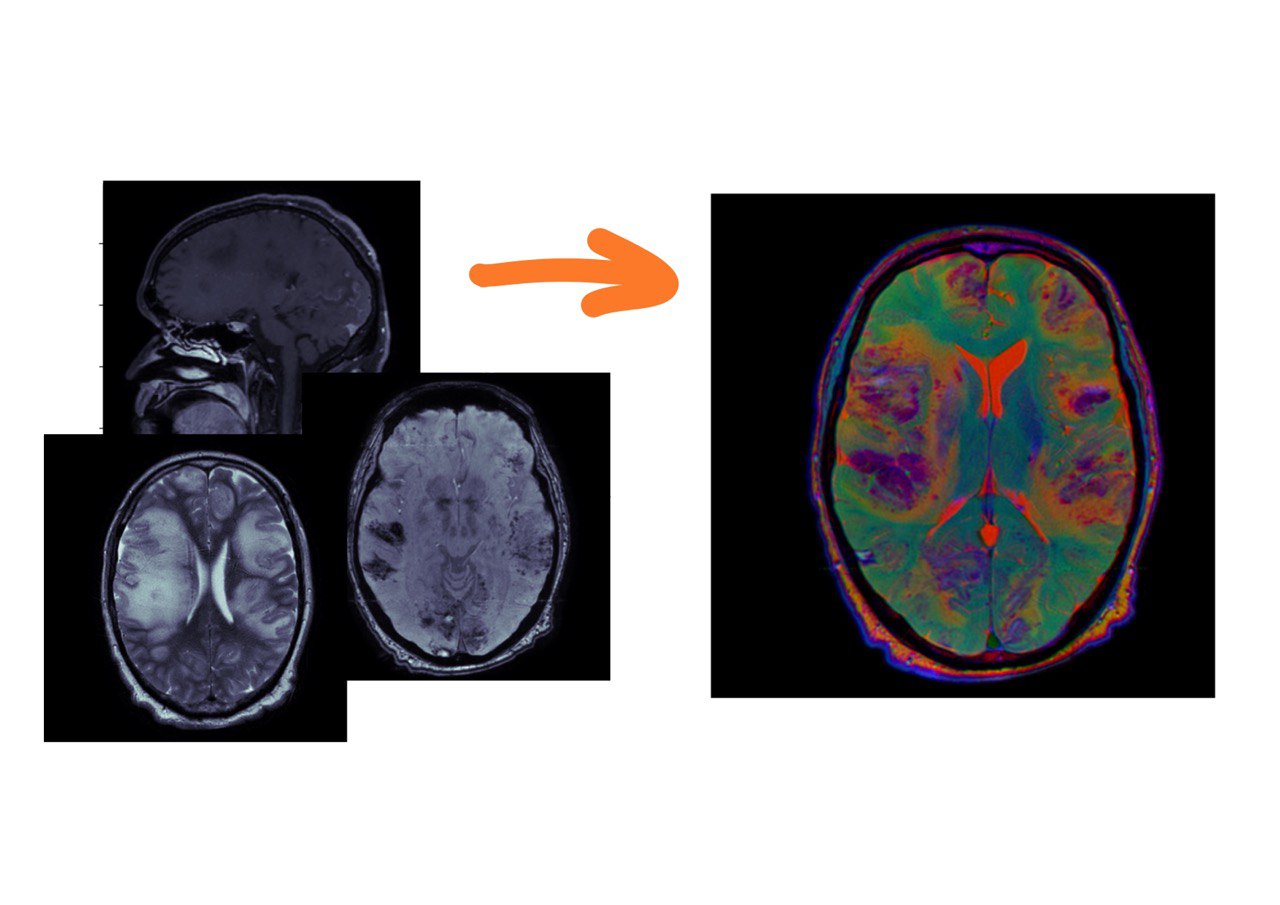
Ресемплинг

Для наглядности я взял T1 с контрастным усилением, SWI и T2. Т1-взвешенная серия нарезана сагиттально, SWI и Т2 – аксиально.

import os
import glob
import pydicom
import numpy as np
import nibabel as nib
from PIL import Image
import SimpleITK as sitk
import matplotlib.pyplot as plt

resample_dir = '.'
glob.glob(f'{resample_dir}/**')

>> ['. \\\\\\mri_resampling.ipynb',
 '. \\\\\\SWI',
 '. \\\\\\T1_CE',
 '. \\\\\\T2']

fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(16,6))
axs[0].imshow(pydicom.dcmread(f'{resample_dir}/T1_CE/IMG-0003-00140.dcm').pixel_array, cmap='bone')
axs[1].imshow(pydicom.dcmread(f'{resample_dir}/SWI/IMG-0005-00046.dcm').pixel_array, cmap='bone')
axs[2].imshow(pydicom.dcmread(f'{resample_dir}/T2/IMG-0002-00030.dcm').pixel_array, cmap='bone')

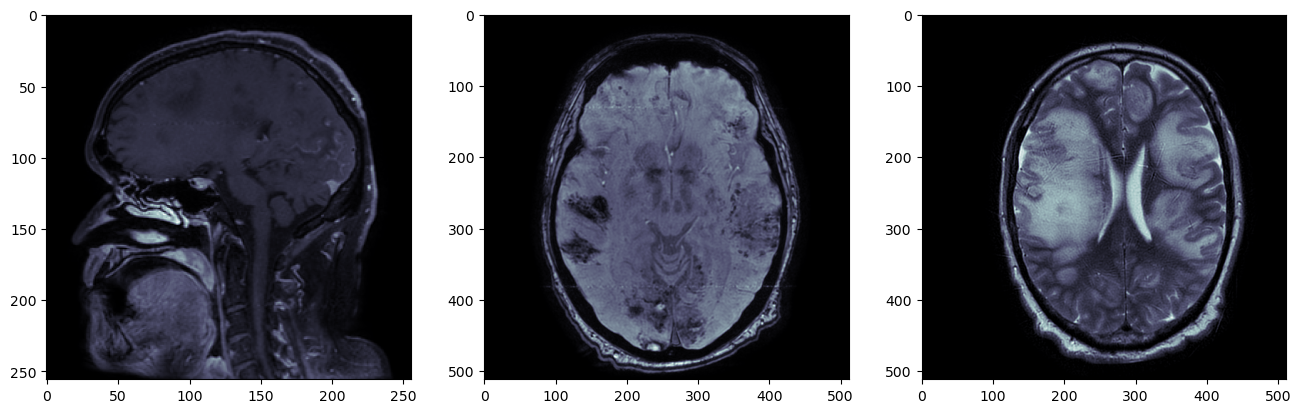
Три серии

Каждая из этих серий содержит полезную информацию, и мы хотим показывать нейросетке все три взвешенности. Для этого их нужно подавать как каналы (примерно так, как делал фотографии Прокудин-Горский в начале 20 века: делал три фотографии через разные светофильтры, а потом накладывал их друг на друга).

Прокудин-Горский

Понятно, что для этого серии должны быть ориентированы идентичным образом. Сейчас покажу, как это можно сделать.

1. (не слишком важный раздел) Матрица аффинной трансформации и простой ресемплинг 🔗

Каждый DICOM-файл хранит информацию о его ориентации в пространстве томографа (которое, в сущности, является частью реального мира с центром координатной сетки в изоцентре МРТ).

Давайте сконвертируем одну из томографических серий в NIfTI-файл, чтобы это стало наиболее наглядно.

reader = sitk.ImageSeriesReader()
reader.LoadPrivateTagsOn()

filenamesDICOM = reader.GetGDCMSeriesFileNames('T2')
reader.SetFileNames(filenamesDICOM)
t2_sitk = reader.Execute()

sitk.WriteImage(t2_sitk,'t2.nii')

После конвертации в NIfTI можно открыть этот файл с помощью библиотеки Nibabel. В ее объекте nibabel.nifti1.Nifti1Image много всего интересного, но две главных составляющих - воксельный массив и матрица аффинного преобразования.

t2_nib = nib.load('t2.nii')
t2_nib_array = t2_nib.get_fdata() #воксельный массив
t2_nib_array.shape

>> (512, 512, 48) - такая размерность у массива

plt.imshow(t2_nib_array[:,:,t2_nib_array.shape[2]//2], cmap='gray')

t2

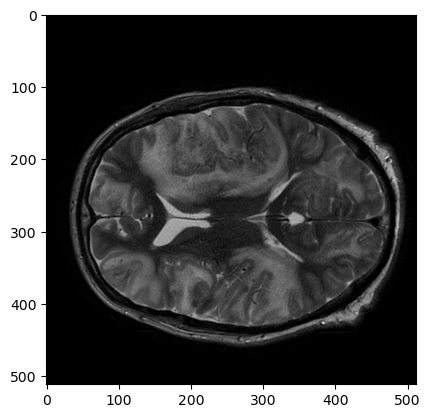
Это воксельный массив. Его расположение в пространстве томографа представлено в матрице аффинного преобразования:

np.set_printoptions(precision=4, suppress=True)
t2_nib.affine

>> array([[ -0.4222,  -0.0167,   0.5434,  99.3905],
          [  0.0131,  -0.429 ,  -0.149 , 143.058 ],
          [  0.0785,  -0.0186,   2.9466, -60.64  ],
          [  0.    ,   0.    ,   0.    ,   1.    ]])

Левая верхняя часть 3х3 содержит информацию о повороте и масштабе. Четвертая колонка отражает смещение относительно центра магнита.

Таким образом, если мы хотим узнать координаты вокселя с индексом [2,5,10] в пространстве томографа, мы можем просто посчитать скалярное произведение левой верхней части матрицы размера 3х3 и поэлементно сложить результат с вектором смещения t (т.е. с четвертым столбцом).

$$ 1) \begin{bmatrix} A_{ 00 } & A_{ 01 } & A_{ 02 } \\\ A_{ 10 } & A_{ 11 } & A_{ 12 } \\\ A_{ 20 } & A_{ 21 } & A_{ 22 }\end{bmatrix} \cdot \begin{bmatrix} { b_0 } \\\ { b_1 } \\\ { b_2 } \end{bmatrix} = \begin{bmatrix} A_{ 00 } \\\ A_{ 10 } \\\ A_{ 20 } \end{bmatrix} \cdot { b_0 } + \begin{bmatrix} A_{ 01 } \\\ A_{ 11 } \\\ A_{ 21 } \end{bmatrix} \cdot { b_1 } + \begin{bmatrix} A_{ 02 } \\\ A_{ 12 } \\\ A_{ 22 } \end{bmatrix} \cdot { b_2 } = \begin{bmatrix} A_{ 00 } { b_0 } + A_{ 01 } { b_1 } + A_{ 02 } { b_2 } \\\ A_{ 10 } { b_0 } + A_{ 11 } { b_1 } + A_{ 12 } { b_2 } \\\ A_{ 20 } { b_0 } + A_{ 21 } { b_1 } + A_{ 22 } { b_2 } \end{bmatrix} = \begin{bmatrix} { x_0 } \\\ { x_1 } \\\ { x_2 } \end{bmatrix} $$

$$ 2) \begin{bmatrix} { x_0 } \\\ { x_1 } \\\ { x_2 } \end{bmatrix} + \begin{bmatrix} { t_0 } \\\ { t_1 } \\\ { t_2 } \end{bmatrix} = \begin{bmatrix} { x_0+t_0 } \\\ { x_1+t_1 } \\\ { x_2+t_2 } \end{bmatrix} = \begin{bmatrix} a \\\ { b } \\\ { c } \end{bmatrix} $$

t2_nib.affine[:3,:3] @ np.array([2,5,10]) + t2_nib.affine[:3,3]

>>array([103.89633372, 139.44894546, -31.10983373])

Последняя строка матрицы аффиного преобразования в дикомах всегда [0,0,0,1], как в единичной матрице. Это нужно просто для того, чтобы сделать матрицу квадратной, тогда ее можно будет использовать как линейный оператор.

t2_nib.affine @ np.array([2,5,10,1]) #(просто добавили единицу как четвертую координату)

>> array([103.89633372, 139.44894546, -31.10983373,   1.        ])

Очевидно, все отдельно взятые сканы головного мозга в пределах одного исследования привязаны к пространству томогрфа, а значит можно их ресемплировать в общее воксельное пространство.

filenamesDICOM = reader.GetGDCMSeriesFileNames('T1_CE')
reader.SetFileNames(filenamesDICOM)
t1_sitk = reader.Execute()
sitk.WriteImage(t1_sitk,'t1.nii')

t1_nib = nib.load('t1.nii')
t1_nib_array = t1_nib.get_fdata()

plt.figure(figsize=(12,6))
plt.subplot(121)
plt.imshow(t1_nib_array[:,:,t1_nib_array.shape[2]//2])
plt.subplot(122)
plt.imshow(t2_nib_array[:,:,t2_nib_array.shape[2]//2])

t1t2

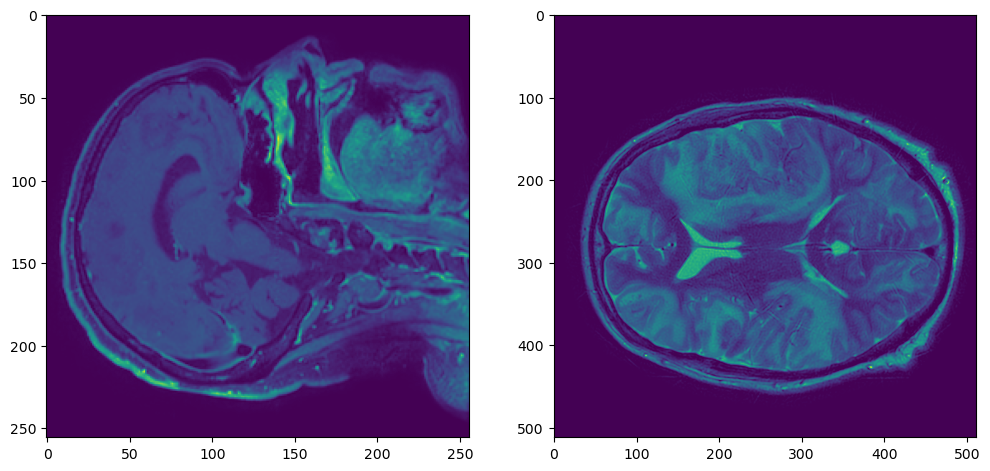
Давайте воспользуемся для этого готовой функцией resample_img из библиотеки nilearn.

from nilearn.image import resample_img

%%time 
t1_resampled = resample_img(t1_nib, target_affine=t2_nib.affine, target_shape=t2_nib.shape)
t1_resampled_array = t1_resampled.get_fdata()

>> CPU times: total: 13.6 s
Wall time: 14.6 s

plt.figure(figsize=(12,6))
plt.subplot(121)
plt.imshow(t2_nib_array[:,:,t2_nib_array.shape[2]//2])
plt.subplot(122)
plt.imshow(t1_resampled_array[:,:,t1_resampled_array.shape[2]//2])

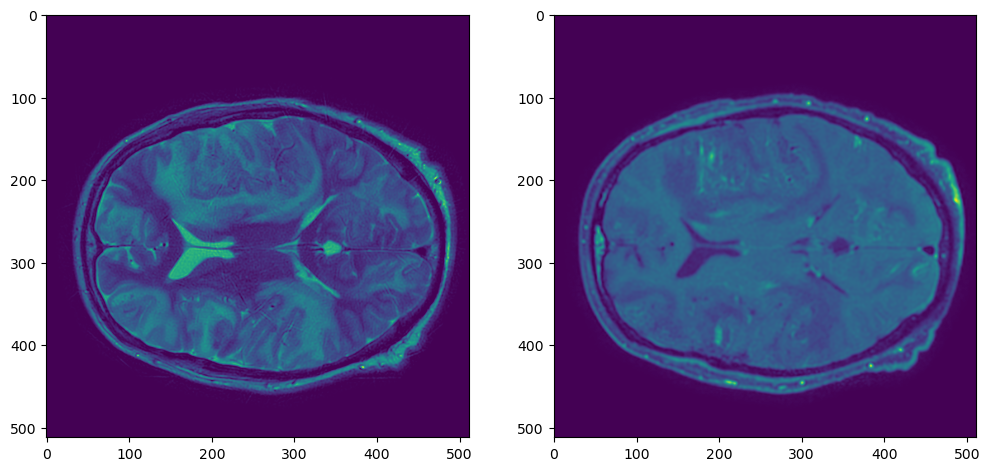
t1t2resampled

Работает довольно медленно, но есть решение быстрее.

2. Ресемплинг с SimpleITK 🔗

filenamesDICOM = reader.GetGDCMSeriesFileNames('T2')
reader.SetFileNames(filenamesDICOM)
t2_sitk = reader.Execute()
t2_sitk

>> <SimpleITK.SimpleITK.Image; proxy of <Swig Object of type 'std::vector< itk::simple::Image >::value_type *' at 0x000002CF0A1E1090> >

Объект SimpleITK.SimpleITK.Image библиотеки SimpleITK также содержит информацию об ориентации вокселей в реальном мире. Но она хранится не в одной удобной матрице аффинной трансформации, а по кусочкам.

t2_sitk.GetOrigin() # то же самое, что четвертый столбец, только с минусом

>> (-99.3905, -143.058, -60.64)

t2_sitk.GetSpacing() # то есть насколько далеко каждый отдельный воксель начинается относительно соседнего по каждой оси

>> (0.429688, 0.429688, 3.0000070292848084)

t2_sitk.GetDirection() # расплющенная косинусная матрица, задающая вращение воксельного облака относительно реального мира

>>  (0.9826872663587349,
     0.03894401075470161,
     -0.18113282574601006,
     -0.03040569918977931,
     0.9983022756891978,
     0.04967957136036232,
     0.18276003390560375,
     -0.04331201196096025,
     0.9822030541729729)

В принципе, все то же самое можно достать и из матрицы аффинной трансформации. Ну например, зная, что каждый ее столбец влияет на одну координату вокселя, можно посчитать маштабирование (т.е. спейсинг, расстояние между началами вокселей). Это обычная евклидова норма.

x_scale = np.linalg.norm(t2_nib.affine[:,0])
y_scale = np.linalg.norm(t2_nib.affine[:,1])
z_scale = np.linalg.norm(t2_nib.affine[:,2])
print(x_scale, y_scale, z_scale)

>> 0.42968800290830866 0.4296879971521231 3.0000068992676026

Очевидно, если разделить каждый столбец на значение спейсинга, то получится косинусная матрица.

t2_pure_rotation = np.hstack((t2_nib.affine[:,0].reshape(-1,1)/x_scale,
                   t2_nib.affine[:,1].reshape(-1,1)/y_scale,
                   t2_nib.affine[:,2].reshape(-1,1)/z_scale,
                   t2_nib.affine[:,3].reshape(-1,1)))
t2_pure_rotation[:3,:3]

>>  array([[-0.9827, -0.0389,  0.1811],
           [ 0.0304, -0.9983, -0.0497],
           [ 0.1828, -0.0433,  0.9822]])

Первые две строки отличаются по знаку от значений в косинусной матрице из SimpleITK. Не уверен, почему так происходит. Может, потому что подразумевается обратное направление координатной оси.

Кстати, эта информация может быть получена и напрямую из DICOM-файлов. Там есть специальный тег для этого.

cosine_from_dcm = pydicom.dcmread(filenamesDICOM[1]).ImageOrientationPatient
cosine_from_dcm

>> [0.982687, -0.030406, 0.182760, 0.038944, 0.998302, -0.043312]

Как видите, он хранит информацию только о двух строках (6 чисел вместо 9). Это ничего, ведь мы можем вычислить третью строку. Она перпендикулярна векторам первых двух строк, так что требуется просто посчитать их векторное произведение:

np.cross(cosine_from_dcm[:3], cosine_from_dcm[3:])

>> array([-0.1811,  0.0497,  0.9822])

Вернемся к ресемплингу. В SimpleITK он организован чуть сложнее, чем в nilearn, но все равно довольно самоочевиден.

def resample(image, ref_image):

    resampler = sitk.ResampleImageFilter()
    resampler.SetReferenceImage(ref_image)
    resampler.SetInterpolator(sitk.sitkLinear)
    
    resampler.SetTransform(sitk.AffineTransform(image.GetDimension()))

    resampler.SetOutputSpacing(ref_image.GetSpacing())

    resampler.SetSize(ref_image.GetSize())

    resampler.SetOutputDirection(ref_image.GetDirection())

    resampler.SetOutputOrigin(ref_image.GetOrigin())

    resampler.SetDefaultPixelValue(image.GetPixelIDValue())

    resamped_image = resampler.Execute(image)
    
    return resamped_image

%%time
t1_resampled = resample(t1_sitk, t2_sitk)

t2_sitk_array = sitk.GetArrayFromImage(t2_sitk)
t1_resampled_array = sitk.GetArrayFromImage(t1_resampled)

plt.figure(figsize=(12,6))
plt.subplot(121)
plt.imshow(t2_sitk_array[t2_sitk_array.shape[0]//2,:,:])
plt.subplot(122)
plt.imshow(t1_resampled_array[t1_resampled_array.shape[0]//2,:,:])

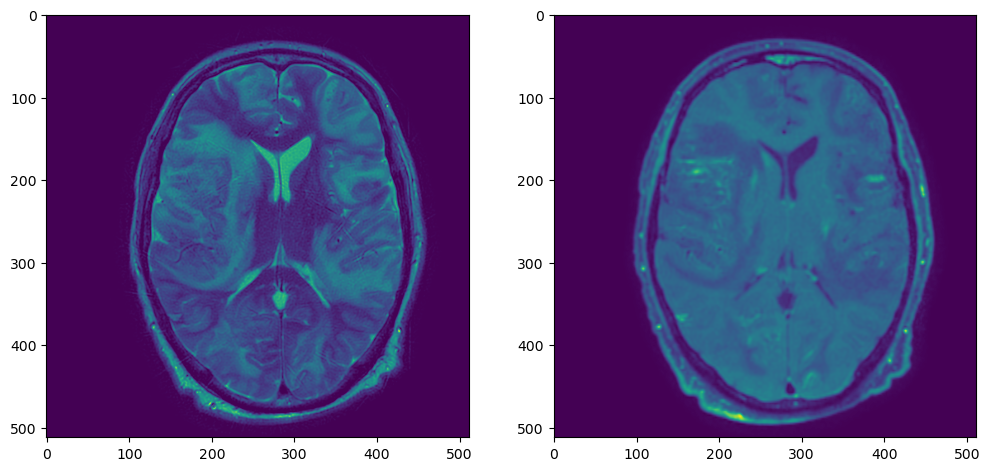
t2t1resampled

Работает гораздо быстрее:

def normalize(data):
    return (data - np.min(data)) / (np.max(data) - np.min(data))

%%time
filenamesDICOM = reader.GetGDCMSeriesFileNames('T1_CE')
reader.SetFileNames(filenamesDICOM)
t1_sitk = reader.Execute()

filenamesDICOM = reader.GetGDCMSeriesFileNames('SWI')
reader.SetFileNames(filenamesDICOM)
swi_sitk = reader.Execute()

filenamesDICOM = reader.GetGDCMSeriesFileNames('T2')
reader.SetFileNames(filenamesDICOM)
t2_sitk = reader.Execute()

swi_resampled = resample(swi_sitk, t2_sitk)
t1_resampled = resample(t1_sitk, t2_sitk)

t2_sitk_array = normalize(sitk.GetArrayFromImage(t2_sitk))
swi_resampled_array = normalize(sitk.GetArrayFromImage(swi_resampled))
t1_resampled_array = normalize(sitk.GetArrayFromImage(t1_resampled))

stacked = np.stack([t2_sitk_array, swi_resampled_array, t1_resampled_array,])

to_rgb = stacked[:,t2_sitk_array.shape[0]//2,:,:].transpose(1,2,0)
im = Image.fromarray((to_rgb * 255).astype(np.uint8))
im

>>CPU times: total: 5.02 s
Wall time: 3.52 s

final

мрт ресемплинг